二 百分数(二) - (4)利率
第1题
A B C
第2题
(1)100000×4%×3=12000(元)
(2)100000+12000=112000(元)
第3题
500×3.25%×1=16.25(元)
第4题
分析:本题可以运用逆推法解答,根据“到期时取出本金和利息共33825元”,可先求出利息是(33825-30000)元,再根据“利息÷本金÷时间=利率”求出年利率。也可以列方程解答,根据等量关系式“本金+利息=33825”和“利息=本金×利率×时间”设年利率是x,可以列出方程30000+30000×x×3=33825,解得x=4.25%。
解答:【方法一】 33825-30000=3825(元)…………(5分)
3825÷30000÷3=4.25%…………(9分)
【方法二】 解:设年利率是x。…………(2分)
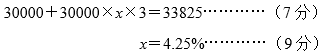
答:年利率是4.25%。…………(10分)
第5题
分析:本题考查了利率在生活中的实际应用。存款时因选择的方式不同,所得的利息也不同,本题要分别算出不同方案所得的利息。
方案一:由题目可知,本金为5000元,存款时间为两年,年利率为3.75%,根据利息=本金×利率×时间,可求得利息=5000×3.75%×2=375(元)。方案二:因选择连续存款,存款时间分别为1年,年利率是3.25%,但是这两年的本金不同,第一年的本金是5000元,第二年的本金是(5000+第一年的利息),所以第一年的利息为5000×3.25%×1=162.5(元),第二年的利息为(5000+162.5)×3.25%×1=5162.5×3.25%≈167.8(元),所以方案二的利息为162.5+167.8=330.3(元)。因为375>330.3,所以按方案一存款合算。
解答:方案一:
5000×3.75%×2…………(2分)
=10000×3.75%
=375(元)…………(3分)
方案二:因连续存款,分年算。
第一年:5000×3.25%×1…………(4分)
=162.5(元)…………(5分)
第二年:(5000+162.5)×3.25%×1…………(6分)
=5162.5×3.25%×1
≈167.8(元)…………(7分)
162.5+167.8=330.3(元)…………(8分)
因为375>330.3,所以按方案一存款合算。…………(9分)
答:按方案一存款合算。…………(10分)
