1.圆柱 - (4)圆柱的体积(一)
第1题
(1)高 底面积 底面积×高 底面积×高 V=Sh (2)300
第2题
(1)√ (2)× (3)√ (4)× (5)×
第3题
(1)B (2)B
第4题
(1)3.14×(18÷2)2×15=3815.1(cm3)
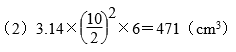
第5题
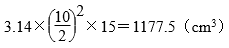
第6题
80 mm=8 cm 5 mm=0.5 cm
第7题
分析:本题考查了物体形状变化后体积不变的知识点。由长方体钢坯熔铸成圆柱体时,变化的是物体的形状,不变的是物体的体积,即V长方体=V圆柱,而V长方体=长×宽×高=31.4×20×4=2512(cm3),V圆柱=底面积×高。
解答:熔铸前长方体钢坯的体积:
31.4×20×4…………(3分)
=2512(cm3)…………(4分)
熔铸后圆柱的高:
2512÷(3.14×42)…………(6分)
=2512÷50.24
=50(cm)…………(7分)
答:圆柱的高是50 cm。…………(8分)
第8题
(答案不唯一)
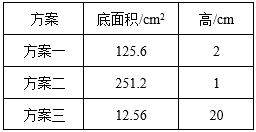
第9题
(1)内圆柱的体积…………(2分)
(2)3.14×42×50 3.14×32×50 1099………(每空6分)
(3)【方法一】 分析:根据求圆柱的体积公式V圆柱=底面积×高=π×半径2×高,要先求出钢管底面内外圆的半径,然后计算内外圆柱的体积差,就是钢管的体积。
解答:10÷2=5(cm)………………(1分)
8÷2=4(cm)………………(2分)
3.14×52×50-3.14×42×50………………(4分)
=3.14×25×50-3.14×16×50
=3925-2512
=1413(cm3)………………(6分)
【方法二】 分析:先求钢管底面的环形面积,再求体积。
解答:(3.14×52-3.14×42)×50………………(4分)
=3.14×9×50
=1413(cm3)………………(6分)
答:钢管的体积是1413 cm3。…………(7分)
第10题
分析:由图①变成图②,减少的表面积就是一个小圆柱的侧面积,圆柱的侧面积=底面周长×高,所以 ,由此可以先求出一个小圆柱的高为314÷(2×3.14×10)=5(cm),再求出搭成的大圆柱的体积,体积=底面积×高,即3.14×102×(5×3)=4710(cm3)。
,由此可以先求出一个小圆柱的高为314÷(2×3.14×10)=5(cm),再求出搭成的大圆柱的体积,体积=底面积×高,即3.14×102×(5×3)=4710(cm3)。
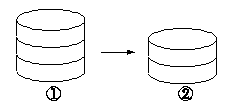
解答:314÷(2×3.14×10)=5(cm)…………(5分)
3.14×102×(5×3)=4710(cm3)…………(9分)
