(一)数与代数 - 2.数的认识(二)
第1题
(1)10 4 30 80
(2)加上6(或乘2)
(3)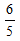
(4)2
第2题
(1)B
(2)C
(3)分析:本题考查了分数的基本性质。
方法一:根据“甲数的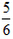 等于乙数的
等于乙数的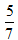 ”可列出算式甲×
”可列出算式甲×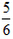 =乙×
=乙×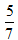 ,因为
,因为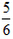 >
>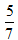 ,所以甲<乙。
,所以甲<乙。
方法二:根据题目可写出比例式: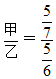 ,再解比例:
,再解比例: ,所以甲<乙。
,所以甲<乙。
解答:B。
(4)C
第3题
(1)6.350 6.3500
(2)5.400 5.40
(3)
不变 十分之一(或0.1)
千分之一(或0.001)
第4题
20.7 103.08 37.808 1083.07 42.408 7.042
第5题

第6题
(1)C (2)A (3)B
第7题
(1)×
(2)×
(3)√
(4)√
(5)√
第8题
分析:本题考查对小数点位置移动引起小数大小变化规律的理解与掌握。
方法一:由乙数的小数点向左移动两位后正好等于甲数可知,乙数是甲数的100倍,所以乙数减甲数的差正好是甲数的99倍,而乙数又比甲数多29.7,说明29.7正好是甲数的99倍,进而就能求出甲数、乙数及两数的和。也可以先求出甲数,因为乙数是甲数的100倍,所以甲数与乙数的和正好是甲数的(1+100)倍,即两数之和为0.3×(1+100)=30.3。
解答:
29.7÷(100-1)=0.3…………(2分)
0.3+0.3×100=30.3或
0.3×(1+100)=30.3……………(2分)
答:甲数与乙数的和是30.3。…………(1分)
方法二:列方程解答。先根据乙数比甲数多29.7,设甲数为x,乙数为(x+29.7),再根据乙数的小数点向左移动两位后正好等于甲数,可列出等式,即乙÷100=甲,然后解方程求出甲数,最后算出乙数和甲数与乙数的和。
解答:
解:设甲数为x,则乙数为(x+29.7)。…………(1分)
(x+29.7)÷100=x………………………… (1分)
0.01x+0.297=x
0.99x=0.297
x=0.3 ……………………… (1分)
0.3+29.7=30
0.3+30=30.3………(1分)
答:甲数与乙数的和是30.3。…………(1分)
第9题
分析:本题考查了分数的基本性质。
方法一:原分数化简后是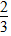 ,把
,把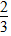 转化成2:3,即2+3=5(份),又因为分子和分母的和是90与5份相对应,所以用90÷5得每份数是18,再求出分子为18×2=36,分母18×3=54,所以原分数为
转化成2:3,即2+3=5(份),又因为分子和分母的和是90与5份相对应,所以用90÷5得每份数是18,再求出分子为18×2=36,分母18×3=54,所以原分数为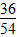 。
。
解答:
3+2=5…………(1分)
90÷5=18…………(2分)
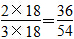 …………(2分)
…………(2分)
答:这个分数原来是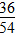 。…………(1分)
。…………(1分)
方法二:列方程解答,可设分数的分子为x,则分母为(90-x),可列方程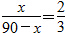 。
。
解答:
解:设分数的分子为x,则分母为(90-x)。
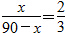 …………(1分)
…………(1分)
3x=(90-x)×2…………(1分)
5x=180
x=36…………(2分)
90-36=54…………(1分)
答:这个分数原来是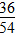 。…………(1分)
。…………(1分)
第10题
分析:本题考查学生对分数基本性质的掌握情况。
方法一:从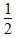 入手,先把
入手,先把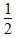 化成分子为7的真分数是
化成分子为7的真分数是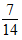 ,根据分子相同,分母小的分数值反而大的规律,可写出大于
,根据分子相同,分母小的分数值反而大的规律,可写出大于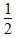 且分子为7的最简真分数有
且分子为7的最简真分数有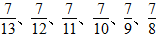 ,共6个,其中
,共6个,其中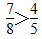 ,不符合题意要求,其余5个最简真分数为正确答案。
,不符合题意要求,其余5个最简真分数为正确答案。
解答: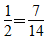 …………(2分)
…………(2分)
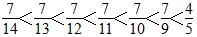 …………(3分)
…………(3分)
答:有5个,分别是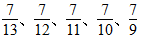 。……(2分)
。……(2分)
方法二:题中3个分数不相等,但是分子已知,可以根据分数的基本性质化成分子相同的分数,即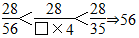 >□×4>35,所14>□>8,因此□可以是13、12、11、10、9,那么符合题意的最简真分数为
>□×4>35,所14>□>8,因此□可以是13、12、11、10、9,那么符合题意的最简真分数为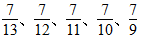 。
。
解答:
 …………(3分)
…………(3分)
因为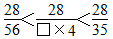 ,所以□可以是13、12、11、10、9。…………(2分)
,所以□可以是13、12、11、10、9。…………(2分)
答:有5个,分别是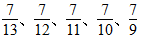 。……(2分)
。……(2分)
