六年级数学（上册） - 练习十五
1.
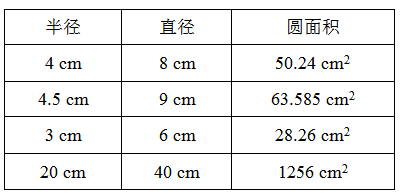
2.左图：3.14×10＝31.4(cm)
3．14×(10÷2)2＝78.5(cm2)
右图：2×3.14×3＝18.84(cm)
3．14×32＝28.26(cm2)
3．分析：喷灌的面积是以喷灌装置为圆心，10 m为半径的圆的面积。
解答：3.14×102＝314(m2)
4．3.14×(125.6÷3.14÷2)2＝1256(cm2)
5．3.14×[(18÷2)2－(7÷2)2]＝215.875(cm2)
6．3.14×62－3.14×(6÷2)2＝84.78(cm2)
7．左图：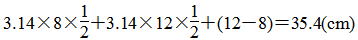
右图：3.14×(122－82)＝251.2(cm2)
8．略
9．3.14×(22.5÷2)2－6×6＝361.40625(mm2)
10．周长：2×3.14×32＋100×2＝400.96(m)
面积：3.14×322＋100×(32×2)＝9615.36(m2)
11．周长：3.14×1×2＝6.28(m)
面积：3.14×(1÷2)2×2＋1×1＝2.57(m2)
12．圭峰楼：3.14×[(33÷2)2－(14÷2)2]＝701.005(m2)
德逊楼：3.14×[(26.4÷2)2－(14.4÷2)2]＝384.336(m2)
相差面积：701.005－384.336＝316.669(m2)
13．分析：面积增加的部分为圆环的面积。
解答：62.8÷3.14÷2＝10(m)
10＋2＝12(m)
3．14×(122－102)＝138.16(m2)
14．分析：由图可知，3分线的长度等于圆周长的一半与两条平行线段的长度之和；3分线内区域的面积等于半圆的面积与长方形的面积之和。已知圆的半径为6.75 m；长方形的长是半圆的直径，宽是1.575 m。
解答：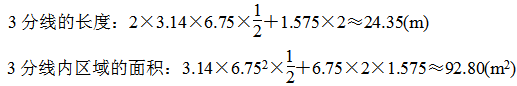
15*.略
16*.分析：如果围成正方形，正方形的边长是31.4÷4＝7.85(m)，面积是7.85×7.85＝61.6225(m2)；如果围成圆，圆的面积是3.14×(31.4÷3.14÷2)2＝78.5(m2)，也可以围成其他四边形。如果围成长方形，长和宽的差越小，面积越大，例如，长是7.9 m，宽是7.8 m时，面积是7.9×7.8＝61.62(m2)；周长相等的长方形与平行四边形无法比较面积，还可以围成三角形、梯形……但无论怎样围，都不会大于围成的圆的面积。
解答：当周长一定时，圆的面积最大，因此应该用这根绳子围成一个圆。
17*.当周长一定时，所有图形中圆的面积最大。蒙古包的底面做成圆形的，可以使居住的面积最大，绝大多数的根和茎的横截面是圆形的，可以最大面积地吸收水分。(合理即可)