四 比 - (3)比的应用
第1题
(1)5 4 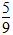
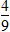
(2)5∶8 48 30
(3)24 36
(4)10 90
第2题
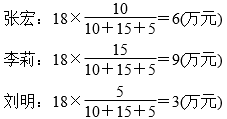
第3题
(1)B
(2)分析:因为三角形的内角和为180°,且三角形的三个内角的度数比是2∶3∶4,也就是把三角形的内角和平均分成2+3+4=9(份),三个内角分别占内角和的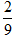 ,
,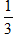 ,
,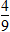 ,所以这个三角形的三个内角的度数分别为
,所以这个三角形的三个内角的度数分别为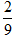 ×180°=40°,
×180°=40°,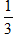 ×180°=60°,
×180°=60°,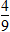 ×180°=80°,所以这个三角形是锐角三角形。选A。
×180°=80°,所以这个三角形是锐角三角形。选A。
解答:A……………………(3分)
(3)B (4)A
(5)因为红球比蓝球多180个,红球与蓝球的个数比是7∶5,也就是红球比蓝球多2份,所以其中1份为180÷(7-5)=90(个),所以蓝球的个数是180÷(7-5)×5,所以选C。
解答:C ……………………(3分)
第6题
分析:已知被减数是150,减数与差的比是3∶2,因为被减数=减数+差,所以可以把被减数看作整体,则减数占整体的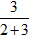 ,差占整体的
,差占整体的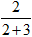 ,所以减数是150×
,所以减数是150×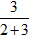 =90,差是150×
=90,差是150×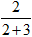 =60。
=60。
解答:减数是150×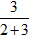 =90……………………(4分)
=90……………………(4分)
差是150×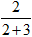 =60………………………(8分)
=60………………………(8分)
答:减数是90,差是60。………………………(9分)
第7题
分析:(1)因为假设这两瓶同样多的药水每瓶都是108L,第一瓶药液与水的体积比是1∶8,也就是药液占总体积的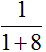 ,所以第一瓶药水中药液的体积是108×
,所以第一瓶药水中药液的体积是108×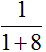 =12(L);第二瓶药水中药液与水的体积比是5∶7,也就是药液占总体积的
=12(L);第二瓶药水中药液与水的体积比是5∶7,也就是药液占总体积的 ,所以第二瓶药水中药液的体积是108×
,所以第二瓶药水中药液的体积是108× =45(L);
=45(L);
(2)两瓶药水中药液的体积为12+45=57(L),两瓶药水的体积为108×2=216(L),所以两瓶药水中药液的体积÷两瓶药水的体积=57÷216=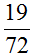 ;
;
(3)同理可求第一瓶药水中药液的体积是108×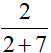 =24(L),两瓶药水中药液的体积为24+45=69(L),所以两瓶药水中药液的体积÷两瓶药水的体积=69÷216=
=24(L),两瓶药水中药液的体积为24+45=69(L),所以两瓶药水中药液的体积÷两瓶药水的体积=69÷216=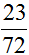 。
。
解答:(1)12 45 ……………………(2分)
(2)57 216 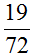 ……………………(5分)
……………………(5分)
(3)69÷216=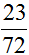 ……………………(12分)
……………………(12分)
第8题
分析:因为乘客A付的车费与其他三位付的车费的比是1:2,也就是乘客A付的车费占总车费的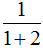 ;因为乘客B付的车费与其他三位付的车费的比是1:3,也就是乘客B付的车费占总车费的
;因为乘客B付的车费与其他三位付的车费的比是1:3,也就是乘客B付的车费占总车费的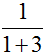 ;因为乘客C付的车费与其他三位付的车费的比是1:4,也就是乘客C付的车费占总车费的
;因为乘客C付的车费与其他三位付的车费的比是1:4,也就是乘客C付的车费占总车费的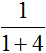 ;所以乘客D付的车费占总车费的
;所以乘客D付的车费占总车费的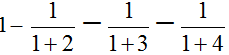 ,而乘客D付了26元,形成对应关系,所以总车费为26÷
,而乘客D付了26元,形成对应关系,所以总车费为26÷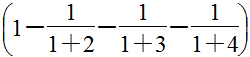 =120(元)。
=120(元)。
解答:26÷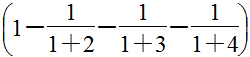 =120(元)………………(8分)
=120(元)………………(8分)
答:这四位乘客一共付车费120元。……………………(9分)
第9题
分析:这是一道方案题,甲队有42人,乙队有18人,甲、乙两队的人数比是42∶18=7∶3=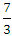 ,现在要使甲、乙两队的人数比是3∶2。
,现在要使甲、乙两队的人数比是3∶2。
方案1:乙队人数不变,减少甲队人数。因为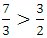 ,若乙队人数不变,减少甲队人数,则甲、乙两队的人数比要比变小,能达到
,若乙队人数不变,减少甲队人数,则甲、乙两队的人数比要比变小,能达到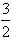 ,所以此方案可行,甲队要减少42-
,所以此方案可行,甲队要减少42-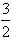 ×18=15(人);
×18=15(人);
方案2:乙队人数不变,增加甲队人数。因为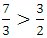 ,若乙队人数不变,增加甲队人数,则甲、乙两队的人数比要变大,不可能达到
,若乙队人数不变,增加甲队人数,则甲、乙两队的人数比要变大,不可能达到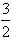 ,所以此方案不可行;
,所以此方案不可行;
方案3:甲队人数不变,减少乙队人数。因为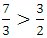 ,若甲队人数不变,减少乙队人数,则甲、乙两队的人数比要变大,不可能达到
,若甲队人数不变,减少乙队人数,则甲、乙两队的人数比要变大,不可能达到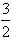 ,所以此方案不可行;
,所以此方案不可行;
方案4:甲队人数不变,增加乙队人数。因为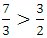 ,若甲队人数不变,增加乙队人数,则甲、乙两队的人数比要变小,能达到
,若甲队人数不变,增加乙队人数,则甲、乙两队的人数比要变小,能达到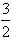 ,所以此方案可行,乙队要增加42÷
,所以此方案可行,乙队要增加42÷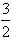 -18=10(人);
-18=10(人);
方案5:将甲队部分人调往乙队。因为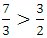 ,若将甲队部分人调往乙队,则甲、乙两队的人数比要变小,能达到
,若将甲队部分人调往乙队,则甲、乙两队的人数比要变小,能达到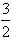 ,所以此方案可行,设将甲队x人调往乙队,甲队现有(42-x)人,乙队现有(18+x )人,根据题意得
,所以此方案可行,设将甲队x人调往乙队,甲队现有(42-x)人,乙队现有(18+x )人,根据题意得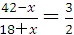 ,解得x=6。
,解得x=6。
方案6:将乙队部分人调往甲队。因为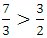 ,若将乙队部分人调往甲队,则甲、乙两队的人数比要变大,不可能达到
,若将乙队部分人调往甲队,则甲、乙两队的人数比要变大,不可能达到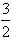 ,所以此方案不可行。
,所以此方案不可行。
解答:方案1:√ 15 ………………(2分)
方案2:×……………………(3分)
方案3:× ……………………(4分)
方案4:√ 10……………………(6分)
方案5:√ 6……………………(8分)
方案6: × ……………………(9分)
&http_url=http://edit.taozhi.cn/phone_a/65061.htm&http_referer=&http_response_type=html&other_client_id=afca9953-1b53-4277-a3e3-f3ae6f374cf3&page_title=%EF%BC%883%EF%BC%89%E6%AF%94%E7%9A%84%E5%BA%94%E7%94%A8&client_type=PC%E7%BD%91%E7%AB%99&br_screen_height=720&br_screen_width=1280&br_platform=Linux%20x86_64&br_app_name=Netscape&page_load_time=1300&con_user_open_id=undefined)
