1.倒数的认识 - 精版答案
第1题
(1)倒数 倒数 (2)乘积
第2题
(1)C (2)B (3)A
第3题
(1)7 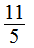 8 (2)0 1
8 (2)0 1
第4题
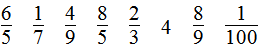
第5题
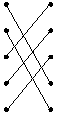
第6题
(1)× (2)× (3)√ (4)√ (5)×
第7题
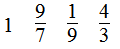
第8题
分析:本题考查的是倒数的性质。举例:当a=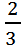 时,a的倒数是
时,a的倒数是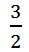 ,当a=
,当a=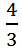 时,a的倒数是
时,a的倒数是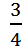 ;当a=1时,a的倒数是1。所以当a大于0且小于1时,a的倒数一定大于a;当a大于1时,a的倒数一定小于a;当a等于1时,a的倒数一定等于a。
;当a=1时,a的倒数是1。所以当a大于0且小于1时,a的倒数一定大于a;当a大于1时,a的倒数一定小于a;当a等于1时,a的倒数一定等于a。
解答:
(1)大于0且小于1 …………………(2分)
(2)大于1 …………………(4分)
(2)等于1 …………………(6分)
第9题
分析:两个数相乘,其中一个因数等于积乘另一个因数的倒数。本题中由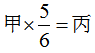 可推出甲=丙×
可推出甲=丙×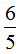 ,所以丙<甲;由乙×
,所以丙<甲;由乙×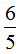 =丙可推出乙=丙×
=丙可推出乙=丙× ,所以丙>乙。
,所以丙>乙。
解答:
乙<丙<甲 …………………(5分)
第10题
分析:(1)一个数的倒数在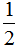 和
和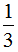 之间,在
之间,在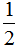 和
和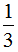 之间的数有无数个,如
之间的数有无数个,如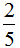 ,
,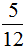 ,…写出其中一个,取其倒数即为所求。(2)一个自然数与它的倒数的和是5.2,这个自然数的倒数一定小于1,所以这个自然数的倒数为0.2,得出这个自然数是5。
,…写出其中一个,取其倒数即为所求。(2)一个自然数与它的倒数的和是5.2,这个自然数的倒数一定小于1,所以这个自然数的倒数为0.2,得出这个自然数是5。
解答:
(1)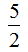 (答案不唯一) ………………(6分)
(答案不唯一) ………………(6分)
(2)5 …………………(12分)
第11题
分析:本题考查的是倒数的意义。乘积是1的两个数互为倒数,所以互为倒数的两个数的乘积是1。因为a、b互为倒数,所以ab=1。由此可知,(1)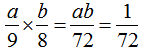 ;(2)
;(2)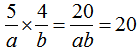 ;(3)
;(3)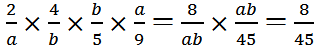 。
。
解答:
(1)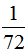 …………………(2分)
…………………(2分)
(2)20 …………………(4分)
(3)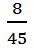 ………………(6分)
………………(6分)
第12题
分析:因为两个连续奇数的倒数的差的分母是195,所以这两个连续奇数的最小公倍数是195,先把195分解质因数,即195=3×5×13,且3×5×13可以改写成15×13,由此可以初步判定这两个连续的奇数是13和15。用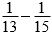 进行验证,结果等于
进行验证,结果等于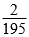 ,所以判定这两个连续的奇数是13和15。同理,因为两个连续奇数的倒数的差的分母是255,所以这两个连续奇数的最小公倍数是255,先把255分解质因数,即255=3×5×17,且3×5×17可以改写成15×17,由此可以初步判定这两个连续的奇数是15和17。用
,所以判定这两个连续的奇数是13和15。同理,因为两个连续奇数的倒数的差的分母是255,所以这两个连续奇数的最小公倍数是255,先把255分解质因数,即255=3×5×17,且3×5×17可以改写成15×17,由此可以初步判定这两个连续的奇数是15和17。用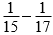 进行验证,结果等于
进行验证,结果等于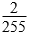 ,所以判定这两个连续的奇数是15和17。
,所以判定这两个连续的奇数是15和17。
解答:
(1)13 15 …………………(4分)
(2)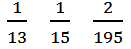 13 15 …………………(14分)
13 15 …………………(14分)
(3)15和17 …………………(18分)
&http_url=http://edit.taozhi.cn/phone_a/65072.htm&http_referer=&http_response_type=html&other_client_id=b9601f81-ffe7-4fa5-be95-8430c7c17b03&page_title=%E7%B2%BE%E7%89%88%E7%AD%94%E6%A1%88&client_type=PC%E7%BD%91%E7%AB%99&br_screen_height=720&br_screen_width=1280&br_platform=Linux%20x86_64&br_app_name=Netscape&page_load_time=602&con_user_open_id=undefined)
